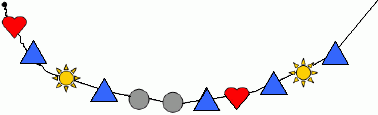
A Marta está a fazer um colar com peças de vários feitios. Mas está a executá-lo de uma forma regular. Reparem:

• Que peça irá a Marta colocar a seguir ao triângulo azul?
• Se ela usar, no total, 63 peças, de quantos corações vai precisar?
• E de quantos triângulos?
• E de quantos círculos?
Resolução
Este problema pode ser resolvido de
duas formas: (1) desenha-se o colar completo e contam-se as peças de cada tipo;
ou (2) fazem-se cálculos para determinar o número de peças das várias espécies.
Mas, quer para resolver o problema pelo desenho, quer para resolvê-lo pelo
cálculo, é necessário perceber como é que o colar se constrói, como é que as
peças se seguem umas às outras. E isto porque a Marta não quer um colar
qualquer, quer um colar regular!
Quando se escreve a sequência 2-8-0-7-1-9-8-7-3-4-2-7-... esta não apresenta
qualquer regularidade e, por isso, não podemos saber qual o número que se segue
ao último 7. Mas se a sequência for 1-3-5-2-4-1-3-5-2-4-1-3-..., toda a gente
pode "adivinhar" que ao último 3 se segue um 5 e depois um 2, etc. Esta segunda
sequência é regular, segue um padrão.
Qual é, então, o padrão do colar da Marta? Vejamos o que diz o Juan Rachadell da
E.B. 2,3 Das Naus, Lagos:
"Ao fazer o colar de 63 peças, a
Marta vai repetir o padrão de 7 peças (Coração Vermelho, Triângulo Azul, Sol
Amarelo, Triângulo Azul, 2 Círculos Cinzentos e Triângulo Azul)".
É este, então, o padrão, a
sequência, que se vai repetir. E quantas vezes se repete esta sequência? A Ana
Filipa Silva, o António Pica e o Fábio Alves da E.B. 2,3 de Vila Nova de S.
Bento, escrevem assim:
"63:7=9 (o número 7 representa as
peças que existem em cada sequência). Num colar de 63 peças existem 9
sequências."
Falta, agora, calcular o número de
peças de cada tipo. Vamos seguir o raciocínio da Ana Catarina Lourenço da E.B.
2,3 D. Martinho Castelo Branco, Portimão:
"Se ela usar, no total, 63 peças,
faz nove sequências. Como em cada sequência há um coração, vai precisar de 9
corações. Como em cada sequência há 3 triângulos, para as nove sequências (63
peças) vai precisar de 27 triângulos. Em cada sequência há dois círculos, nas
nove vezes (63 peças), vai precisar de 18 círculos".
Mas quem remata bem o problema é a
Joana Teigão da EB 2,3 D. Afonso III, Faro:
"Mas se pensarmos que ela já
iniciou o colar e que nos mostra na figura, podemos dizer que ... precisa de 7
corações. Os 9 do total para o colar menos os 2 que aparecem na figura.
... precisa de 22 triângulos. Os 27 do total para o colar menos os 5 que
aparecem na figura.
... precisa de 16 círculos. Os 18 do total para o colar menos os 2 que aparecem
na figura".
Bem, e então qual é a peça que se
segue às que vemos na figura? Como diz a Joana Teigão:
"Na figura aparece-nos uma
sequência e 4 peças da sequência seguinte: coração – triângulo – sol –
triângulo. A peça que virá a seguir será um círculo".
Os alunos que desenharam os colares enviaram-nos alguns lindos! Queremos destacar o colar do Ventsislav Nikolov e do Stanislav Osovschi da E.B. 2,3 Infante D. Fernando, Vila Nova de Cacela, bem como o das alunas Daniela Rita, Jéssica Cavaco e Raquel Dourado da E.B.I. Professor Doutor Aníbal Cavaco Silva, Boliqueime.