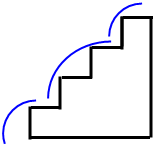
Os avós do Miguel têm uma quinta e vivem aí, numa casa antiga, onde há muitas escadas. Nas férias, o Miguel vai sempre passar uns dias na quinta dos avós. Quando está cansado, o Miguel sobe um degrau de cada vez, mas quando tem pressa, sobe os de graus dois a dois. Às vezes, mistura estas duas formas de subir as escadas. A figura que se segue mostra duas maneiras diferentes de subir uma escada com 4 degraus:


1. Há outras maneiras de subir esta escada? Em caso afirmativo, qual ou quais?
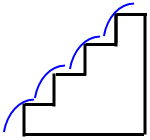
2. De quantas maneiras diferentes pode o Miguel subir uma escada com 3 degraus? Faz um desenho ilustrativo.
3. E se a escada tiver 5 degraus? Ilustra a resposta.
4. E se o Miguel também conseguisse subir 3 degraus de cada vez, de quantas formas diferentes poderia subir a escada com 5 degraus? Faz um desenho ilustrativo.
Resolução
Este problema requeria, apenas, atenção ou, melhor ainda método na procura das respostas. Isto para que não escapasse nenhuma delas!
Uma forma simples de encontrar as respostas que foi, por exemplo, utilizada pelo Olekxandr Panchenko da E.B. 2,3 de Quarteira e pelo Ivan Alzugaray da E.B. 2,3 Padre Cabanita, Loulé, consistia em transformar o problema num problema numérico.
Assim, para a pergunta 1, o método consistia em encontrar todas as decomposições do número 4, utilizando, apenas, o 1 e o 2:
1-1-1-1; 2-1-1; 1-2-1; 1-1-2; 2-2
Utilizando o mesmo método, teríamos as seguintes respostas:
Resposta à pergunta 3: 1-1-1; 1-2; 2-1.
Resposta à pergunta 4: 1-1-1-1-1; 2-1-1-1; 1-2-1-1; 1-1-2-1; 1-1-1-2 (têm três 1 e um 2, vai-se mudando a posição do 2); 2-2-1; 2-1-2; 1-2-2 (têm dois 2 e um1, vai-se mudando a posição do 1).
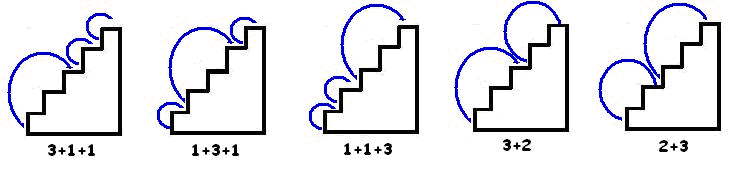
Resposta à pergunta 5: Além das oito formas anteriores, poderia ainda subir de mais cinco formas diferentes: 3-1-1; 1-3-1; 1-1-3 (faz-se variar a posição do 3); 3-2; 2-3.
E, depois, faziam-se os desenhos. Ora vejam os desenhos da Ana Silva, do António Pica e do Fábio Alves da E.B. 2,3 de Vila Nova de S. Bento.