Premiados

 

	1º Classificado João Francisco Ramalho EB 2,3 Nº 1 de Reguengos de Monsaraz
	2º Classificado Ana Sofia Guerreiro EB 2,3 Padre João Coelho Cabanita Loulé
	3º Classificado Gonçalo Tomás Jacob EB 2,3 Dr. José Neves Júnior Faro

 

 

 

 

Vídeo

 

 

 

 

 

Álbum

 

 

 

 

 

Finalistas

 

 

 

 

Programa da final (em PDF)

 

 

 

 

 

Palestra

 

Criatividade, imaginação e intuição… porque nem só de cálculo vive a matemática

 

Prof.ª Doutora Isabel Vale, Instituto Politécnico de Viana do Castelo.

 

 

 

 

Calcular, memorizar, treinar são aspetos indiscutivelmente ligados à matemática, mas a matemática é muito mais. Estas são as suas componentes mais vulgarizadas e menos interessantes, pois não contribuem para a formação integral do aluno nem são desafiadoras. Tarefas que exijam a utilização e o relacionamento de conhecimentos previamente adquiridos, que desafiem os alunos a descobrir padrões, a fazer conjeturas, a fazer demonstrações, a recorrer a desenhos e a diferentes materiais, constituem a atividade matemática. Contribuem para o desenvolvimento de formas mais elaboradas de raciocínio e tornam os jovens curiosos, críticos, criativos e, acima de tudo, mais hábeis na resolução de problemas.

 

 

 

 

Prémios

 

1º classificado:
- Uma conta poupança CaixaProjeto no valor de 50 €, oferta da CGD.
- Uma experiência Dolphin Emotions, oferta do Zoomarine.
- Uma lapiseira, oferta do centro de cópias Central.

- Um cheque-livro, no valor de 10 €, oferta da Bertrand.
 
2º classificado:
- Uma conta poupança CaixaProjeto, no valor de 30 €, oferta da CGD.
- Uma entrada no Zoomarine, oferta do Zoomarine.
- Uma lapiseira, oferta do centro de cópias Central.

- Um cheque-livro, no valor de 10 €, oferta da Bertrand.
 
3º classificado:
- Uma conta poupança CaixaProjeto, no valor de 20 €, oferta da CGD.
- Uma entrada no Zoomarine, oferta do Zoomarine.
- Uma lapiseira, oferta do centro de cópias Central.

- Um cheque-livro, no valor de 10 €, oferta da Bertrand.

 

 

 

Patrocinadores:

 

Caixa Geral de Depósitos

Zoomarine

Centro de cópias Central

Bertrand

 

 

Um restaurante de hambúrgueres vendeu 363 hambúrgueres durante o fim de semana. Os clientes do restaurante podem pedir no máximo 3 molhos no seu hambúrguer: maionese, mostarda e ketchup. Dos hambúrgueres vendidos, 92 tinham apenas maionese e 94 tinham maionese e mais um ou dois molhos. Houve 82 hambúrgueres que levaram mostarda e mais um ou dois molhos mas 58 tinham apenas ketchup e mostarda. Foram vendidos 63 hambúrgueres que só tinham mostarda e 17 que tinham apenas mostarda e maionese. Não houve nenhum hambúrguer vendido sem molho.
Quantos dos hambúrgueres vendidos tinham apenas ketchup?

 

Não te esqueças de explicar o teu processo de resolução.

 

 

 

Um comerciante comprou um lote de T-shirts turísticas para vender na sua loja de souvenirs. No primeiro mês conseguiu vender 1/3 das T-shirts com um lucro de 10%, pelo valor de 660 euros. Por azar, teve depois uma inundação na loja e 1/4 das restantes T-shirts ficaram um pouco danificadas. Essas, decidiu vendê-las por metade do preço de compra.
Se o comerciante quiser recuperar o valor que pagou pelo total das T-shirts, que margem de lucro deverá incluir no preço das T-shirts que não foram atingidas pela inundação?

 

Não te esqueças de explicar o teu processo de resolução.

 

 

 

Cinco amigas decidiram que era hora de perderam peso e de voltarem ao seu peso ideal. Então decidiram todas começar a fazer dieta e um programa de exercício físico com grande sucesso. Uns meses mais tarde, cada uma das amigas tinha atingido a sua meta que era perder entre 6 e 10 quilos! Determina o nome completo de cada amiga e os seus pesos antes e depois da dieta e da ginástica.

1. A Sara, cujo apelido não é Almeida, perdeu mais peso do que a Natália.
2. A Paula passou do peso de 58 quilos para o peso final de 50 quilos.
3. A outra mulher que perdeu 8 quilos foi a Sra. Martins cujo peso final foi de 52 quilos.
4. A Sra. Cardoso, cujo primeiro nome não é Paula, terminou a sua perda de peso com 66 quilos.
5. A mulher que perdeu menos peso começou com 61 quilos.
6. A Sra. Veiga perdeu 10 quilos.
7. A Mariana começou com o maior peso, que era 75 quilos, mas não terminou com o maior peso final.
8. Sara terminou a sua perda de peso com 52 quilos.
9. A Clarisse Nunes não foi a que terminou com o peso de 65 quilos.

 

Não te esqueças de explicar o teu processo de resolução.

 

 

 

 

A Joana estava a ler um livro de aventuras e no final disse aos seus amigos:

- O livro que acabei de ler tinha tantas páginas que a soma dos dígitos de todos os números das páginas é 1198!

Quantas páginas tinha o livro que a Joana leu?

 

Não te esqueças de explicar o teu processo de resolução.

 

 

 

Num congresso de professores de Matemática estiveram presentes 270 participantes. Todas as conferências decorreram em três anfiteatros: A, B e C.
Durante a manhã, os participantes distribuíram-se pelos três anfiteatros de acordo com os assuntos que lhes interessavam.
Na parte da tarde, metade das pessoas que estiveram de manhã no anfiteatro A passaram para o B. Um quarto das pessoas que estiveram de manhã no anfiteatro B passaram para o C. Um terço das pessoas que estiveram de manhã no anfiteatro C passaram para o A.
Apesar das mudanças, o número de pessoas que esteve em cada anfiteatro não se alterou da manhã para a tarde.
Quantos participantes estiveram em cada um dos anfiteatros?

 

Não te esqueças de explicar o teu processo de resolução.

 

 

 

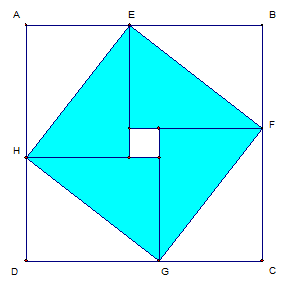
Na figura dada, ABCD é um quadrado com 10 cm de lado.
Sabe-se que e que a região pintada de azul tem uma área de 32 cm², sendo formada por quatro triângulos retângulos.
Quanto mede ?

 

Não te esqueças de explicar o teu processo de resolução.

 

 

 

O Eduardo e o Jaime fizeram 4 testes de Matemática no período passado, que foram classificados de 0 a 100 pontos.
As médias das classificações que eles obtiveram nos 4 testes foram iguais.
O Jaime teve mais 10 pontos no 1.º teste do que o Eduardo e teve menos 15 pontos do que o Eduardo no 2.º teste. No 3.º teste, as classificações de ambos foram iguais. No 4.º teste o Jaime teve 70 pontos.

Qual foi a classificação do Eduardo no 4º teste?

 

Não te esqueças de explicar o teu processo de resolução.

 

 

 

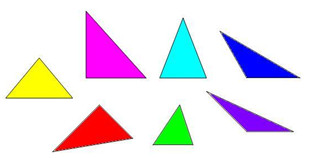
O Luís marcou 10 pontos de modo que não ficassem três sobre uma mesma reta. Em seguida numerou-os de um a 10. Quantos triângulos existem com vértices nesses pontos, em que a soma dos números é ímpar?

 

Não te esqueças de explicar o teu processo de resolução.

 

 

 

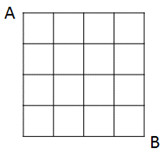
Imagina que precisas de te deslocar do canto superior esquerdo da grelha (A) até ao canto inferior direito (B). Para o fazeres só podes percorrer os lados dos quadrados unitários em duas direções: para baixo e para a direita.
Na grelha de 4 por 4, quantos caminhos podes escolher para ires de A até B?

 

Não te esqueças de explicar o teu processo de resolução.

 

 

 

 

No Salão da Sociedade Recreativa foi organizado um espetáculo de Natal. Depois de terminada a festa, os jovens voluntários tiveram a tarefa de arrumar as cadeiras da plateia.
Quando as empilharam em pilhas de 11, sobrou 1 cadeira.
Quando as empilharam em pilhas de 12, sobraram 6 cadeiras.
Quando as empilharam em pilhas de 13, sobraram 12 cadeiras.
O número de cadeiras era superior a 800 mas não chegava a 1000.

Quantas cadeiras havia para arrumar no final do espetáculo?

 

Não te esqueças de explicar o teu processo de resolução.